TGM is a coherent dozenal metric system - a complete
metrology devised for the dozenal system, better designed and
integrated than is the decimal metric system. It was devised and
developed by Tom Pendlebury, a member of the Dozenal Society of
Great Britain (DSGB).
In its original form it was a trial booklet issued with Dozenal
Review *26, and no more than twenty pages long, but later
reissued in an enlarged form with tables and additional units,
running to over six dozen pages. It would seem sensible, in these
days of electronic publishing, to reissue the booklet, using PDF
format, via the Web. Our audience being so much greater on the
Web, we hope there will be more comments and feedback than were
possible in the past.
Links to reviews of TGM and comments (for and against) appear at the end of this section.
This Introduction tells you how the system is constructed.
The main details of the system will be presented as PDF documents
(most of which have yet to be rewritten before they can be linked
to these pages) which you can download and read at your leisure.
The reason for using PDF documents is quite simply that the
symbols for ten and eleven, and the font in which they are used,
can be embedded in the documents.
There is no reason why the ones we use in our work should be
considered sacrosanct; we need someone who can design us two
brand new symbols that will fit in with the present set and be
acceptable to all those who use dozenals. Not an easy task - but
there are many people out there on the Web!
Note: we need to distinguish dozenal numbers from decimal;
it has long been our custom to use the asterisk (*) to mark a
dozenal number, and so, for convenience, we will mark the dozenal
numbers where necessary and leave the decimal unmarked.
Many who suggest new systems of metrology start by defining the
unit of length. Tom Pendlebury considered this a mistake. He
began with the unit of time.
TIME
The regular recurrence of night and day is mankind's chief notion
of the passage of time. The day is already divided into two dozen
hours, written dozenally as *20, and for reasons which will
become apparent later, the hour is the major time unit in TGM.
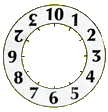
Traditional subdivisions of the hour proceed in
sixties, with minutes and seconds; in a dozenal system they
proceed in twelfths - one twelth of the hour corresponding to
five minutes. Traditional clock and watch faces are marked
off in twelfths of the hour.
Fractions, which are so easy to visualise using a clock face,
have a familiar appearance when written in dozenal instead of
decimal - "quarter past" the hour has the minute hand at the 3 on
the clock face, and one quarter in dozenals is *0·3. Similarly
for half past the minute hand is at the 6, and a half in dozenals
is *0·6.
In order to develop a dozenal metrology and derive a practical
system of weights and measures from the unit of time, that time
unit has to be chosen carefully. The most suitable - and the one
suggested by Tom Pendlebury, is defined as 12-4 of the
hour, or, in dozenals, *0·0001Hr, and this he named the
"TIM".
1 TIM (Tm) = 25/144 seconds (*0·21) = 0·17361111...s and this is the Fundamental Unit of TGM.
The metre and the foot started from origins quite independent of
the unit of time - they are arbitrary. The TGM unit of length is
derived from the TIM by the law of gravity.
Watch a diver leaving a high springboard. His upward velocity
gradually falls off until at the top of his jump he startes to
fall. Down he comes faster and faster until he enters the water.
This changing velocity is called "acceleration due to (Earth's)
gravity". Laboratory tests in vacuum (so no air resistance) show
this acceleration to be the same for all things, large or small,
heavy or light, feather or lump of lead. It is given the symbol
"g".
Its value in our traditional systems is 32·741 ft, or 9·80665 m,
per second per second. It is fundamental to a vast number of
dynamic calculations (though in many cases not obviously so).
In TGM it is made the UNIT of acceleration.
LENGTH
Using Tims instead of seconds, g is just under 30cm per Tim per
Tim. About eleven and five eighth inches, a little short of a
foot. This length is called the Gravity foot or GRAFUT,
abbreviation Gf.
No-one invented it. It is a natural phenomena that comes to light
when reckoning in dozens and hours. Whatever unit of length be
chosen, g would still have to be defined. So let it be the unit itself and have g = 1 Grafut per Tim per Tim.
For the base of a system of measures it must be very accurately
defined; all other units depend on it. Gravity is slightly
stronger at the poles than at the equator. This allows within
very narrow limits a choice of standard best suited for the
rest of the system.
The choice of standard, and all other details not appropriate to
a brief introduction such as this is, will eventually follow in the TGM
booklet.
With the unit of length defined we may also now define the unit of square measure , the square Grafut, or SURF (Sf) and that of volume, the cubic Grafut, or VOLM (Vm). (The names of the units are those created by Tom Pendlebury). We also have the unit of acceleration, the GEE (G) defined as 1 Gf/Tm2, and the unit of velocity the VLOS (Vl) defined as 1 Gf/Tm.
Mass per unit volume is called density. It has been found most practical to compare densities to that of the commonest liquid, water. So our next main unit is the unit of mass:
1 MAZ (Mz) = the mass of 1 Vm of air-free water under a pressure of one standard atmosphere and at the temperature of maximum density (3·98°C).
Tom Pendlebury pointed out that though the Maz is large compared
to the pound or kilogramme, this maintained the 1:1 ratio between
basic units, leaving prefixes to display the sense of proportion.
(These prefixes will be described after the main units have been
described in this introduction. Greater detail will be in the
booklet, including such long strings of figures are are necessary
to cope with the most stringent accuracy that anyone might require).
In metric the gramme came from a cubic centimetre, a
millionth of a cubic metre. The kilogramme (the
basic unit for SI) starts with a built-in prefix meaning
thousand, but has a water volume about a cubic
decimetre, only a thousandth of a cubic metre. In
complex calculations decimal place errors often creep in due to these irregularities.
The unit of Density, the DENZ (Dz) is 1 Mz/Vm, the SG of water.
1 Kg of water at maximum density occupies 1·000028 cubic
decimetres, which was th definition of the "litre" until 1964.
The CGPM then redefined "litre" as the "synonym for cubic
decimetre" but its use "is discouraged for precision
measurements". This irregularity, excluded from TGM causes slight
variances between conversion figures derived from the kilogramme
and others derived from the metre.
It will be appreciated that a complete metric system, whatever number base it is constructed for, will require units to be defined and created for every possible application. All such units, along with auxiliary units have been so defined, and all physical constants (velocity of light etc) defined in terms of the TGM units; any metric system meant to replace the decimal metric system must have all these units and definitions so that the system can be properly evaluated by those who are interested in using it.
Before leaving the topic of the units we will add the unit of
force
1 MAG (Mg) = 1 Mz x 1G
the strength required to hold 1 Mz of anything from falling, the
weight of 1 Mz.
Standing, sitting, lying, walking, jumping, lifting, carrying,
holding, climbing, running upstairs, weight is with us
through every moment of our lives. The only escape is to go into
orbit; then we sense the abnormality or
weightlessness.
TGM preserves the good points of the present rival systems, discarding their flaws and awkward quirks, and brings metrology more in step with natural laws and counting.
We can count without actual digits, but we can't count without words. To be able to describe the units and their multiples we need a dozenal vocabulary. If we count in twelves instead of in tens, do we keep the words "ten" and "eleven", or make up new ones, such as "dek" and "elv" to make it clear we are not using base ten? Whatever the advocates of the dozenal system may suggest, someone will not like the words they choose. The names and words that now follow are those created and proposed for use with dozenals by Tom Pendlebury. They will not please or suit everyone, but they do allow us to describe the units in dozenal terms.
Where we need to use symbols for ten and eleven here in text published on the Web we shall use T for ten and E for eleven. (This is a personal choice, made in the days when special characters had to be soldered into place on typewriter keys...) In booklets and documents written in PDF format, where it is possible to embed special fonts and characters we shall use the symbols shown on the clockface at the beginning of this TGM section. (Alternatives to these symbols are discussed in the Introduction to Dozenals.)
Every second number is a multiple of TWO; every third a multiple of THREE; every fourth a multiple of FOUR, and so on. Because two twos are FOUR, two threes are SIX, two fours are EIGHT, three threes are NINE and three fours are TWELVE it is a natural law that the numbers 2, 3, 4, 6, 8, 9 and twelve play the most dominant roles in calculation. They come through in spite of decimalisation:
2 x 0·2 = 0·4, 2 x 0·3 = 0·6, 2 x 0·4 = 0·8, 3 x 0·3 = 0·9 etc
The lowest common multiple of 0·1, 0·2, 0·3, 0·4 and 0·6 is 1·2, a dozen TENTHS; and if 0·5 is included, the LCM is 6·0, the HALF DOZEN. Whether counting in units, tenths, sixteenths, hundreds, millions or whatever, makes no difference. The dozens still dominate, though this is often not obvious, due to our writing numbers in tens.
Recognition of this truth has led many individuals, from different nations and generations, to the conclusion that calculation and measurement can be more simply expressed by counting, not in tens, but in DOZENS. Yet is we still write twelve as "12", which means 1 ten and 2 units, we are not counting in dozens but in tens. The full benefit can only be achieved by using "10" to mean 1 DOZEN and 0 units.
We count from one to nine as usual, and then have ten (T), eleven
(E) and the dozen (*10); Tom Pendlebury suggested "elv" for
eleven, and "zen" (also "onezen") for *10.
We can continue our count with *11, *12, *13 and so on, read as
"onezen one", "onezen two", "onezen three" up to *20 "twozen",
then *30 "threezen" until we reach *10 x *10, zen times zen, or
*100. The usual name for this is one gross, and though one dozen
times this has the name "great gross" (*1000), there are no other
common names for higher powers of twelve. We need to create new
words, and from them derive the prefixes, like centi-, milli- and
kilo-, which we can attach to the units of any dozenal metric
system we may devise. The names which Tom created for use with
TGM follow.
The following table lists the new words and gives their values in dozenal and in decimal. Putting a nought on in dozenal multiplies by a dozen, just as, in tens spelling, putting a nought on a number multiplies its value by ten. This gives dozenal counterparts of hundreds, thousands and so on that look like them but stand for different values. The job of words is to evoke and distinguish ideas, so these different ideas are given different names - and on a more straightforward basis. They are coined to suggest the index of the order - in simple English, how many noughts to put.
| Name | Dozenal value | Noughts | Standard Form | Decimal equivalent |
|---|---|---|---|---|
| Zen | 10 | 1 | 101 | 12 |
| Duna | 100 = zen x zen | 2 | 102 | 144 |
| Trin | 1 000 = 10x10x10 | 3 | 103 | 1 728 |
| Quedra | 10 000 | 4 | 104 | 20 736 |
| Quen | 100 000 | 5 | 105 | 248 832 |
| Hes | 1 000 000 | 6 | 106 | 2 985 984 |
| Sev | 10 000 000 | 7 | 107 | 35 831 808 |
| Ak | 100 000 000 | 8 | 108 | 429 981 696 |
| Neen | 1 000 000 000 | 9 | 109 | 5 159 780 352 |
| Dex | 10 000 000 000 | T | 10T | 61 917 364 224 |
| Lef | 100 000 000 000 | E | 10E | 743 008 370 688 |
| Zennil | 1000 000 000 000 | 10 | 1010 | 8 916 100 448 256 |
Nevertheless we use numbers to tell us what we cannot figure out without their help. They mainly tell us which is bigger than which, by how much or by what factor. Both in dozenal and decimal "300" is greater than "10" by a factor of "30". But whereas in decimal 3 hundred is thirty times ten, in dozenal 3 gross is three dozen times a dozen - a rather larger ratio on a rather larger number.
Armed with the number names we can define multiplying prefixes, similar to "kilo-" and "mega-"; in TGM they end with the letter -a. Thus, for example, a dozen feet (Gf) can be called the Zenagrafut, *100 years a Dunayear.
Similar to "deci-", "centi-", "milli-" we have dividing prefixes ending in -i. One twelfth of an hour is thus a zenihour, and the Tim (Tm) which we defined earlier, can also be referred to as the Quedrihour.
To avoid any confusion with letters used for decimal prefixes the abbreviations are written as numerals, raised for multipliers and lowered for dividers - e.g. with the Maz (TGM unit of mass), abbreviated Mz:
1 2Mz (1 dunamaz) = 100 Maz; 1 3Mz (1 trinimaz) = 0.001 Maz.
No matter how complex a problem, the order of the magnitude is kept track of by adding and subtracting the prefixes, which are in fact exponents. Duna times duna gives quedra; quena x trina = aka; but quena times trini = duna. In multiplication the "-a"s are added and the "-i"s subtracted. For powers the prefixes are multiplied; the square of quena is dexa. For roots they are divided; the cube root of neeni is trini.
The names themselves may not suit all; but they fdllow a more logical pattern than the current practice in decimal in which a trillion multiplied by a quadrillion comes out to an octillion, which is the cube of a billion, and that billion is no longer the square of a million but the trillion is.... All very confusing, when the English billion is a million million and the American a thousand million (for which the Germans have the word milliard...)
to be continued ...